前分析篇讲的是三段论的分类,构造,以及在辩论、反驳、证明等领域的应用。
三段论的基础
所有三段论都是三个词项,某一词项(中词)和另外两者发生联系作为前提,从而得出另外两者中大词对于小词的关系。因此,总共有四个格:
- AB,BC->AC
- BA,BC->AC
- AB,CB->AC
- BA,CB->AC
其中,任意两者的关系可以划分为全称/特称的从属关系的肯定与否定。具体有
- AaB, A属性属于所有B,或所有的B是A的。(全称肯定)
- AeB, A属性不属于任何B。所有B都不是A的。(全称否定)
- AiB,A属性属于某些B,存在B是A的。(特称肯定)
- AoB, A属性不属于某些B,存在B不是A的。(特称否定)
进一步,前提和结论可以是实然/或然/必然的。对于实然必然的谓词关系,词项的从属关系的置换有:AaB-> AiB, AeB->BeA, AiB->BiA。对于或然的谓词关系,有A pa B -> A pe B, A pi B-> A po B,A pa B -> A pi B,唯一不同的是A pe B 不能得出 B pe A。
最本质的三段论都是第一格的,其余所有三段论都可以通过词项置换以及归谬法产生。具体表格:
实然三段论
| 1. A?B, B?C->A?C | 2. B?A, B?C->A?C | 3. A?B, C?B->A?C | 4. B?A, C?B->A?C |
|---|---|---|---|
| Barbara | Cesare | Datisi | Calemes |
| Celarent | Camestres | Disamis | Dimatis |
| Darii | Festino | Ferison | Ferison |
| Ferio | Baroco | Bocardo | Calemos(r) |
| Barbari(r) | Cesaro(r) | Felapton | Fesapo |
| Celaront(r) | Camestros(r) | Darapii | Bamalip |
必然三段论
| 1. A?B, B?C->A?C | 2. B?A, B?C->A?C | 3. A?B, C?B->A?C | 4. B?A, C?B->A?C |
|---|---|---|---|
| Barbara N.N | Cesare N.N | Datisi N.N | Calemes .NN |
| Celarent N.N | Camestres .NN | Disamis .NN | Dimatis .NN |
| Darii N.N | Festino N.N | Ferison N.N | Ferison N.N |
| Ferio N.N | Baroco .NN | Bocardo | Calemos(r) |
| Barbari(r) | Cesaro(r) | Felapton N.N | Fesapo N.N |
| Celaront(r) | Camestros(r) | Darapii N.N .NN | Bamalip .NN |
或然三段论
| 1. A?B, B?C->A?C | 2. B?A, B?C->A?C | 3. A?B, C?B->A?C | 4. B?A, C?B->A?C |
|---|---|---|---|
| Barbara P.P/.PP/PPP | Cesare .P. | Datisi P.P/.PP/PPP | Calemes P.. |
| Celarent P.P/.P./PPP | Camestres P.. | Disamis P.P/.PP/PPP | Dimatis P.P/.PP/PPP |
| Darii P.P/.PP/PPP | Festino .P. | Ferison .P./PPP/P.P | Ferison .P./PPP/P.P |
| Ferio P.P/.P./PPP | Baroco P.. | BocardoP.P | Calemos(r) |
| Barbari(r) | Cesaro(r) | Felapton P.P | Fesapo P.P |
| Celaront(r) | Camestros(r) | Darapii P.P/.PP/PPP | Bamalip P.P/.PP/PPP |
三段论的常见谬误
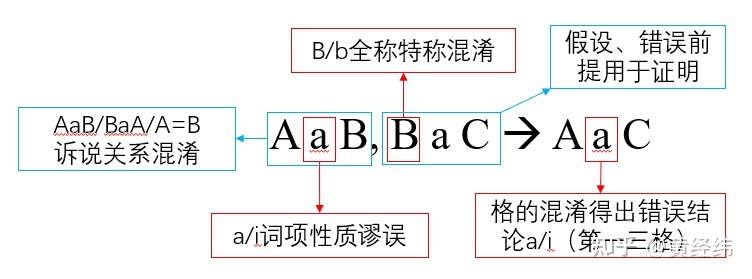
本质上可以分为词的错误、关系的错误、全称/特称的,前提的错误、格的错误。
每个格的使用方法

第一格考虑的是全称的证明与全称反例的反驳,全称的证明只能使用第一格。第二格是用共同的性质描述不同的主体,从而分析不同主体的关系。若性质相同,则是一种从属关系的标示,若性质不同,则至少特称上两者存在不从属的关系。第三格用于特称的反例来反驳第一格的三段论证明。第四格本质上可以转换为其他格。
证明、反驳、辩证的方法论
- 演绎法(Deductive Reasoning),通过三段论顺着推出结论。
- 归纳法(Inductive Reasoning),从特例中找到普遍性,通过普遍性可换位的确认,从而有所有特例的普遍性型的全称三段论证明。
- 例证法(Exemplification),通过两个特例,通过确认两者的等同性,从而有第一格的特称肯定三段论。
- 化简法(Simplification),通过缩小待确定所具有性质的对象的范围,获得更简单的问题。
- 归谬法(Reduction to Absurdity),通过将结论的矛盾命题作为前提和某一前提,推出与另一前提相矛盾的结论,从而得到证明,用于所有格。
- 反驳法(Refutation),通过全称的反例以及特称的反例,通过反例作为中词与原论点的两个主体发生联系,进行第一格和第三格的反驳。
- 标示(Sign),通过两个主题的共性和异性,得到两者可能全称相属和必然特称相异的结论。